티스토리 뷰
1. Binary Tree
Binary Tree는 한개의 Node가 최대 2개의 자식 Node를 갖는 Tree구조를 의미합니다.
Binary Tree를 구현하는 방법은
1. Array를 이용하여 간접구현
2. Class & Struct를 사용한 Pointing 구현
두가지 방법이 있습니다.
Binaray Tree는 이중 두번째, Class를 이용해 Node를 만든고, Node를 이용해 Binary Tree를 만드는 방법입니다.
Binary Tree는 Node를 구성되어 있으며, 이 Node는 left_Node, Value, right_Node로 구성됩니다.
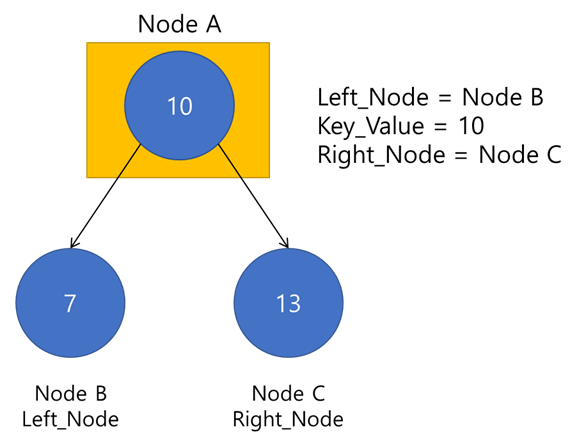
이때 Binary Search Tree는 Key_value를 기준으로 Left_node의 value는 작은값이, Right_node는 큰 값을 갖는 규칙이 있습니다.
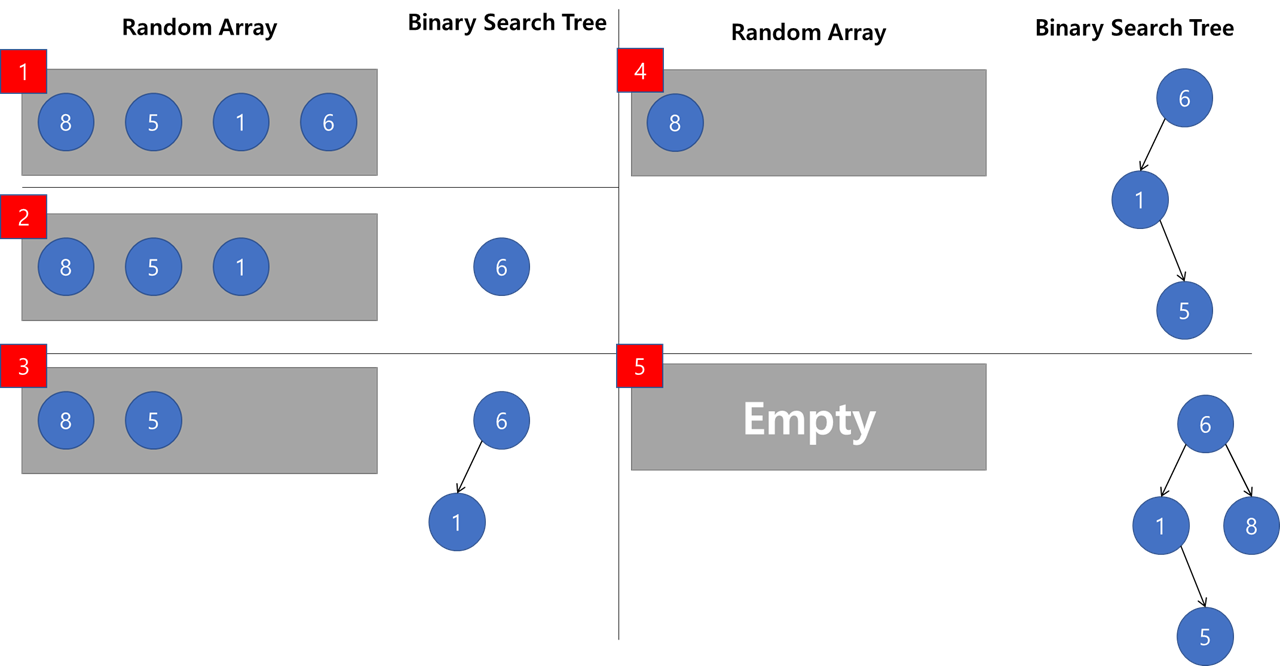
위 규칙을 이용해서 Random Array의 이진 탐색 Tree를 구축합니다.
1. Random Array의 Element 추출
2. Element와 Node와의 값 비교
3_1. Element > Node Value이면 Right Node로 이동
3_2. Element <= Node Value이면 Left Node로 이동
4. Node Value가 None일 때까지 반복
5. Node에 Element 를 입력.
6. 모든 Element에 대해서 1~5 반복
2. Binary Search Tree를 활용한 Search
이제 왼쪽 보단 크고, 오른쪽 보단 작은 Value를 갖는 Binary Search Tree가 완성되었습니다.
이제 Value X가 Binary Search Tree에 있는지 알아보겠습니다.
해당 Node -> Left Node -> Right Node 혹은 Node -> Right Node -> Left Node순으로 각 Node의 Value와 X를 비교하면 Tree 전체를 순회하며 X의 존재 여부를 찾을 수 있습니다.
이때 일반적인 Array에서 비교하는것과 무슨 차이인가? 하는 의문이 들 수 있습니다.
Node기준으로 좌 우의 Value가 규칙이 존재하기 때문에,
Tree의 Depth 만큼만 비교하면 X의 존재여부를 확인할 수 있습니다
이때 완전 Binary Tree의 Depth가 logn의 크기를 가지므로, 평균적인 시간 O(logn)의 시간복잡도를 가집니다.
하지만, Binary Tree가 한쪽으로 쏠릴경우 Depth가 n이 나와 일반 배열과 같은 O(n)의 시간복잡도를 갖습습니다.
때문에 Tree의 Depth를 최소화 하기 위한 Balance Tree구축 방법들이 존재하게 됩니다(추후 다룰예정)
파이썬으로 작성된 Binary Search Tree Code입니다.
import random
#Node Class, Binary 이기 때문에
#left, right, 그리고 현재 Node의 Value를 Attribute로 갖습니다.
class binary_node:
def __init__(self, left_node, key_value, right_node):
self.left_node = left_node
self.key_value = key_value
self.right_node = right_node
class binary_tree:
def __init__(self, DT_list):
self.ori_DT_list = DT_list
#최상위 루트Node
self.start_node = binary_node(None, None, None)
#(없어도 무관)tree의 Node객체를 보관하는 List
self.tree_result = []
#insert_node 매쏘드를 사용해서 List의 모든 Element를
#Binary Tree로 만듭니다.
for i in range(len(DT_list)):
self.insert_node(self.ori_DT_list[i], self.start_node)
#random List를 받아서 Binary Search Tree를 구축합니다
#또는 새로운 Element를 Binary Search Tree에 추가합니다.
def insert_node(self, value, start):
#start가 None이면 최상위 루트Node가 없느것이므로
#최상위 루트Node를 추가합니다.
if start == None:
start = binary_node(None, None, None)
#도달한 Node의 Value가 None이면 Element의 값으로 최신화를 시켜줍니다.
if start.key_value == None:
start.key_value = value
#(없어도 무관)tree의 Node들의 집합을 확인하기 위한 부분
self.tree_result = self.tree_result + [start]
#Element가 Node의 Value보다 작으면 왼쪽으로 가서 동일반복수행
elif start.key_value>value:
if start.left_node == None:
start.left_node = binary_node(None, None, None)
self.insert_node(value, start.left_node)
#Element가 Node의 Value보다 크면 오른쪽으로 가서 동일반복수행
elif start.key_value<=value:
if start.right_node == None:
start.right_node = binary_node(None, None, None)
self.insert_node(value, start.right_node)
#구축된 Binary Tree에 Find_value가 존재하는지 확인합니다
def search(self, find_value, node = 9999):
result = 0
#Class내의 Attribute를 초기값으로 부여하기 위한 Code입니다.
if node == 9999:
node = self.start_node
if node !=None:
#Node의 값과 찾는값이 같으면 Search 종료
if node.key_value == find_value:
return 1
#찾는값이 Node의 Value보다 작으면 왼쪽으로 가서 동일반복수행
if find_value < node.key_value:
result = self.search(find_value,node.left_node) + result
#찾는값이 Node의 Value보다 크면 오른쪽으로 가서 동일반복수행
elif find_value >= node.key_value:
result = self.search(find_value,node.right_node) + result
#모든 탐색 결과 Node값과 찾는 값이 같을경우 result가 0보다 크게 됩니다,
#이점을 활용해서 값의 존재 여부를 Boolean로 반환합니다.
return True if result >= 1 else False
#Random Array 생성
data = [random.randrange(10,60) for i in range(10)]
test = binary_tree(data)
test.search(random.randrange(10,60))
==> Random Value가 Binary Search Tree에 있는지 여부 확인'Python 알고리즘 > 탐색 알고리즘' 카테고리의 다른 글
| Distinct Value Search(Hash탐색) (0) | 2021.02.19 |
|---|---|
| Distinct Value Search(단순탐색) (0) | 2021.02.18 |
| Hash (0) | 2021.02.01 |
| 특정 위치의 값 찾기 (0) | 2021.01.17 |
| Binary Search (0) | 2021.01.16 |
- Total
- Today
- Yesterday
- Python
- Transformer
- SIMD
- git
- 셀프모청
- 이분탐색
- 모바일청첩장
- 자료구조
- Search알고리즘
- Sort알고리즘
- hash
- LLM
- 완전탐색 알고리즘
- react
- ChatGPT
- GDC
- Greedy알고리즘
- 코딩테스트
- stack
- ai
- GPT
- 프로그래머스
- deepseek
- 동적계획법
- 청첩장
- javascript
- prime number
- 알고리즘
- 분할정복
- AVX
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |

