티스토리 뷰
합병정렬 알고리즘은 분할정복방법을 사용한 정렬 알고리즘 입니다.
합병정렬은 정렬을 할 배열을 가장 작은 단위(배열의 Element가 2개만 있을때까지)로 분할하고
분할한 작은 단위의 배열을 정렬하고, 정렬된 배열을 합치고 다시 정렬하는 방법을 사용합니다.

출처 : www.101computing.net/merge-sort-algorithm/
Merge Sort Algorithm | 101 Computing
Computers are often used to process large amounts of data. Some of the tasks they can be used for is to sort data sets in order, e.g. numerical order or alphabetical order. Though this may seem like a simple task to complete, a lot of research has focused
www.101computing.net
알고리즘을 보면, 왜 굳이 나눠서 비교를하고, 다시 합치면서 다시 또 정렬을하지? 생각 할 수 있습니다.
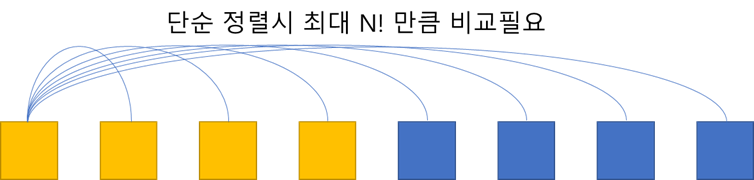

차이가 보이시나요?
분할 후 Merge를 하면서 정렬을 하게되면 비교를 해야할 경우의 수가 감소하면서 시간복잡도가 감소하게됩니다.
때문에 복잡하지만, 분할 후 Merge를 하는 Merge_sort를 사용합니다.
Merge Sort의 시간복잡도는
T(n) = T(n/2) + T(n/2) + Θ(n) (Θ(n)<- Merge소요시간)
= 2*T(n/2) + Θ(n)
이며, 이 점화식을 풀어주면 T(n) = O(nlogn)의 시간복잡도를 갖는 알고리즘인 것을 확인할 수 있습니다.
import random
#Generate ordered List
Data = [i for i in range(10000)]
#Shuffle ordered list
random.shuffle(Data)
def merge_sort(Data):
#부분배열을 나눌 중앙 위치를 확인합니다
mid_loc = round(len(Data)/2)
#index Error 발생 방지
if mid_loc >=1:
#좌측과 우측의 부분배열에 반복적으로 부분배열을 나눕니다.
#이 과정은 left와 right 부분배열이 각각 1개의 원소일때까지 진행됩니다.
left = merge_sort(Data[:mid_loc])
right = merge_sort(Data[mid_loc:])
#부분배열이 1개 원소에 도달하면 이제 적은 Element끼리 비교하여
#정렬된 List를 만들어갑니다.
Data = merge(left,right)
return Data
#부분배열을 가지고 다시 정렬하는 함수를 정의합니다.
def merge(L,R):
#각 부분배열의 첫 원소들을 비교하기 위해서 첫 Index를 미리 할당해줍니다.
left_index = 0
right_index = 0
#왼쪽과 오른쪽 부분배열의 Element 개수만큼의 임시 List를 준비합니다.
#Merge Sort는 추가적인 배열이 요구되는 알고리즘입니다.
temp_list = [0]*(len(L)+len(R))
#Index 0부터 각각 Left와 Right 의 값을 비교해 나갑니다
#비교 후 작은 값을 temp_list로 옮기고, 옮긴 부분배열의 Index를 올려줍니다.
while left_index <len(L) and right_index <len(R):
if L[left_index] < R[right_index]:
temp_list[left_index + right_index]=L[left_index]
left_index = left_index +1
else:
temp_list[left_index + right_index]=R[right_index]
right_index = right_index +1
#위 과정 진행 후 둘중 한 배열의 Index가 남게될 수 있습니다.
#그러면 남은 Index에 해당하는 Element들을 temp_list에 순서대로 적재합니다
#Merge 과정에서 부분배열은 이미 정렬이 되어있기 때문에, 계속 정렬된 순서가 유지됩니다.
#좌측 부분배열이 남았으면 temp_list로 Element 이동
while left_index < len(L):
temp_list[left_index + right_index]=L[left_index]
left_index = left_index +1
#우측 부분배열이 남았으면 temp_list로 Element 이동
while right_index <len(R):
temp_list[left_index + right_index]=R[right_index]
right_index = right_index +1
return temp_list
Data = merge_sort(Data)'Python 알고리즘 > 정렬 알고리즘' 카테고리의 다른 글
| Counting Sort (0) | 2021.02.06 |
|---|---|
| Bubble Sort (0) | 2021.02.05 |
| Heap Sort (0) | 2021.01.22 |
| Insert & Shell Sort (0) | 2021.01.21 |
| Quick Sort (0) | 2021.01.16 |
- Total
- Today
- Yesterday
- Search알고리즘
- ChatGPT
- 완전탐색 알고리즘
- javascript
- 코딩테스트
- AVX
- SIMD
- 이분탐색
- Greedy알고리즘
- 프로그래머스
- 알고리즘
- stack
- GPT
- prime number
- 모바일청첩장
- 셀프모청
- 청첩장
- mcp
- react
- 동적계획법
- deepseek
- git
- 자료구조
- hash
- nlp
- Transformer
- Sort알고리즘
- ai
- Python
- LLM
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
