티스토리 뷰
기하변환?
기하변환이란 기하학적인 좌표계에서 성분의 변화라고 할 수 있습니다.
1. 1차원 좌표계
점을 (x1,y1) -> (x2, y2)로 움직이는것이 가장 기초적인 기하변환 이라고 할 수 있겠죠.

이때 x2 = x1 + delx, y2 = y1 + dely 로 표현됩니다. 이제 이 식을 벡터로 표현하면
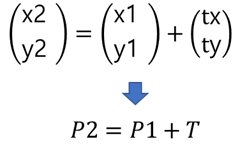
이때, 이 두 점을 원점에서 부터 비교하면, 특정한 점을 원점으로부터 거리만큼의 배수만큼 증가시키는 크기변환은

위와같은 행렬곱을 이용하면, 가로를 a배, 새로를 b배 늘리는 것을 손쉽게 할 수 있습니다 :)
이제 점의 직선의 이동을 했으니, 회전을 생각해봅시다.

원점에서 떨어진 거리가 같을 때, 각도 W에서 V만큼 추가로 회전하는 기하변환 입니다.
이때 반지름을 r이라고하면, x1, y1 과 x2, y2는 모두 r와 삼각함수로 표현이 가능합니다.

위와같이 행렬 곱셈을 통해서, 각도 V만큼의 회전한 위치의 x,y값을 구할 수 있게 됩니다.
2. 3차원 좌표계
이제 2차원 좌표계에서 3차원으로 논리를 확장할 수 있습니다.

위처럼 단순하게 Dimension을 추가함 으로써 손쉽게 구하는 것이 가능합니다.
하지만 회전을 보면, 이야기가 달라집니다.

회전은 2개의 축을 고정하고, 나머지 한개의 축을 기준으로 회전하게 됩니다.
2차원에서는 2개의 축을 고정하면 남은 축이 없이 때문에, 한가지 회전만 가능했지만
3차원 좌표계로 들어오면서 2개의 축을 고정하고 1개로 회전하는 경우의 수가 3개로 늘어납니다.
3차원 좌표계에서는 이 3가지 Case에 대한 회전변환을 정의해야 합니다.

이때 Z axis의 방향이 일반적인것과 다른 이유는
Z축을 고정시킬 경우 2차원 좌표계와 동일하게 하기 위함입니다.(직관성을 위해서!)
이제 3차원 좌표계에서도 기하변환을 정의하였습니다. 이렇게 N차원까지 기하변환이 가능합니다.
이때 점의 이동은 행렬의 덧셈이고, 크기변환과 회전이동은 행렬의 곱을 사용합니다.
매우 불-편 합니다.
다음시간엔 첫시간에 언급했던 동차좌표계를 사용해서 위 수식들을 재 정리하도록 하겠습니다.
아래는 Python으로 구현된 기하변환 입니다 :)
import math
class geo_trans:
def __init__(self, DT_list):
self.data = DT_list
#특별한 축을 입력하지 않을 경우
#회전 평면은 [0,1] = [x,y]입니다.
def oper(self, sort, degree, axis = [0,1]):
#단순 점의 이동인 경우 degree만큼을 각 점마다 더해줍니다.
if sort == "move":
return [(self.data[i]+degree[i]) for i in range(len(self.data))]
elif sort == "mag":
#크기변환을 위한 Matrix를 만들어줍니다.
#변환 Matrix를 nxn형태의 Zero Matrix를 만들어줍니다,
s_mat = [[0 for i in range(len(self.data))] for j in range(len(self.data))]
i = 0
#이때 크기변환 Mat을 만들기 위해서 대각선행렬에
#크기변환 정도만큼의 값을 치환해줍니다.
while True:
s_mat[i][i] = degree[i]
i = i + 1
if i==len(s_mat):
break
#원본 point와 동일한 Dimension을 갖는 Vector Frame을 준비합니다.
temp_result = [0 for i in range(len(self.data))]
#matrix 곱연산을 통해서 크기변환 결과를 구합니다.
for i in range(len(s_mat)):
temp = 0
for j in range(len(s_mat)):
temp = temp + s_mat[i][j]*self.data[j]
temp_result[i] = temp
return temp_result
elif sort == "rot":
#회전의 축에 따라 변환 Matrix가 달라집니다.
#두개의 주어진 축 외에 나머지 축은 고정시키고
#두개의 축의 첫번째가 2차원에서 x, 두번째가 2차원에서 y라고 가정합니다.
r_mat = [[0 for i in range(len(self.data))] for j in range(len(self.data))]
#r_mat에서 대각선 행렬을 모두 1로 초기화합니다.
i=0
while True:
r_mat[i][i] = 1
i = i + 1
if i==len(r_mat):
break
degree = degree/180*math.pi
#일반적인 2차원 좌표계의 Case(↑y+, →x+)
if axis[0]<axis[1]:
r_mat[axis[0]][axis[0]] = math.cos(degree)
r_mat[axis[0]][axis[1]] = -math.sin(degree)
r_mat[axis[1]][axis[0]] = math.sin(degree)
r_mat[axis[1]][axis[1]] = math.cos(degree)
#일반적인 2차원 좌표계에서 x가 reverse된 Case(↑y+, →x-)
elif axis[0]>axis[1]:
r_mat[axis[1]][axis[1]] = math.cos(degree)
r_mat[axis[1]][axis[0]] = -math.sin(degree)
r_mat[axis[0]][axis[1]] = math.sin(degree)
r_mat[axis[0]][axis[0]] = math.cos(degree)
#원본 point와 동일한 Dimension을 갖는 Vector Frame을 준비합니다.
temp_result = [0 for i in range(len(self.data))]
#matrix 곱연산을 통해서 크기변환 결과를 구합니다.
for i in range(len(r_mat)):
temp = 0
for j in range(len(r_mat)):
temp = temp + r_mat[i][j]*self.data[j]
temp_result[i] = temp
return temp_result
import random
test_dt = [random.randint(1, 100) for i in range(10)]
#=>ex. [76,100,10,78,21,43,39,49,31,40]
test = geo_trans(test_dt)
#입력한 좌표들만큼 점의 이동
test.oper("move",[15,9,6,1,3,5,6,7,9,19])
Out[38]: [91, 109, 16, 79, 24, 48, 45, 56, 40, 59]
#입력한 값만큼 각 점마다 크기 변환
test.oper("mag",[1,9,6,8,3,5,6,7,9,19])
Out[39]: [76, 900, 60, 624, 63, 215, 234, 343, 279, 760]
#입력한 차원을 기준으로 회전 변환
test.oper("rot",145,[6,9])
Out[40]: [76, 100, 10, 78, 21, 43, -54.88998718131252, 49, 31, -10.396600753868885]'컴퓨터과학 > 컴퓨터 그래픽스' 카테고리의 다른 글
| 6. 채색 알고리즘(수정중) (0) | 2021.02.15 |
|---|---|
| 5. 기하변환 3(복합기하변환, 아핀변환) (0) | 2021.02.13 |
| 4. 기하변환2(동차좌표ver) (0) | 2021.02.12 |
| 2. 곡선과 원 (0) | 2021.02.10 |
| 1. 점과 선 (0) | 2021.02.09 |
- Total
- Today
- Yesterday
- 코딩테스트
- 모바일청첩장
- 완전탐색 알고리즘
- stack
- 알고리즘
- 동적계획법
- Python
- 병렬처리
- hash
- heap
- Greedy알고리즘
- GDC
- 이분탐색
- 자료구조
- 셀프모청
- react
- SIMD
- 청첩장
- 컴퓨터그래픽스
- Search알고리즘
- AVX
- 분할정복
- 프로그래머스
- C++
- 사칙연산
- prime number
- Sort알고리즘
- git
- javascript
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
