티스토리 뷰
지난 포스팅까지 점과 선의 구성, 변환에 대해서 포스팅하였습니다.
그럼 이제 선과 선 사이에 어떻게 색을 채워넣는지 알아보도록 하겠습니다.
다각형이 있다고 할때, 이 다각형에 수평으로 선을 그으면 대략적인 채색의 윤곽이 보이게됩니다.

보면 알 수 있듯, 수평이 아닌 선분에서 다각형을 그리면 위처럼 접점의 회수가 존재합니다.
이때, 주황색은 색이 칠해질 부분이고, 파란색은 색이 칠해지지 않을 부분이 됩니다.
즉, 접점이 짝수인 부분은 비채색, 접점이 홀수인 부분만 채색을 하게됩니다.
아지만 위 방법만 으로는, 아래와 같은 경우의 채색을 결정하지 못합니다.

수평선분 또는 꼭지점과 만날 경우, 처음에 말씀드린 법칙 만으로는 어느 부분에 채색을 해야할지 알기 어렵습니다.
이 문제를 해결하기 위해서 3가지 법칙이 적용됩니다.
1. 선분이 (x1,y1) (x2,y2)가 연결된 선분일 때, y2>y1 이라면 (x2,y2)는 선분에서 제외
2. x축과 평행한 선분은 없는것으로 취급
3. 교차하는 위치가 x_start ~x_end라면 x_start~x_end -1 까지의 픽셀을 내부픽셀로 정의
위 법칙을 적용해주면, 난해하던 채색방법이 아래처럼 해결됩니다.

보시는것처럼, 상부의 꼭지점을 버리면서 수평 선분과 만나는 지점이 한쪽으로 고정됩니다.
이렇게되면 수평선분 위치의 모호함과 꼭지점에서 판단의 모호함이 모두 사라지게 됩니다.
이제 채색을 할 위치를 판단하는 방법을 정했습니다.
그럼, 이제 해당 알고리즘을 어떻게 컴퓨터로 구현할까 입니다.
이때 자료구조에서 사용했던 연결리스트(Hash Table과 유사한 형태)를 활용해 다각형 선분 테이블을 만들게 됩니다.
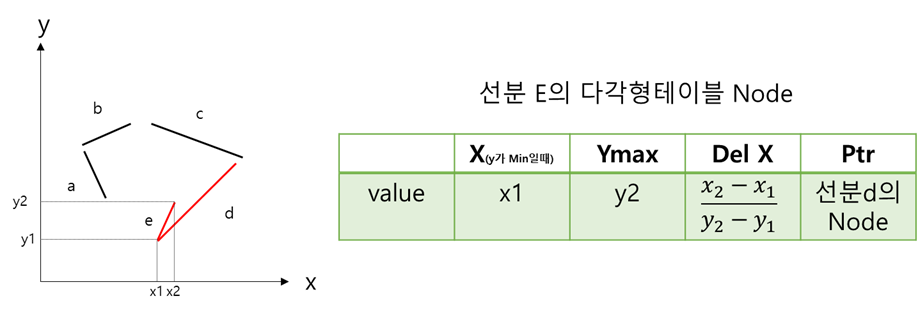
다각형 테이블은 Y값(주사선) 만큼 Index가 존재하며, 각 주자선에 포함되는 Node는
해당 Y값과 꼭지점이 만나는 선분들이 포함되게 됩니다.
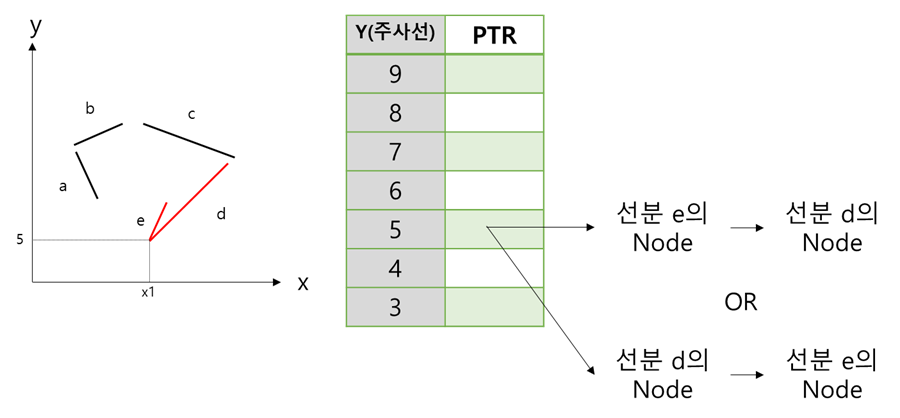
이때 PTR에 추가하는 Node의 X_ymin값이 작은 선분부터 다각형 테이블에 위치하는것이 좋습니다.
수평선과 만나는 Line이 한쪽 기준으로 정렬되어야만
수평선과 선분이 만나는 횟수, 홀-짝을 구분하기 쉽기 때문입니다.
이렇게 하기위해서 아래 규칙을 비교해줍니다.
1. X_ymin값이 작은 선분이 다각형 테이블에 가깝게 추가
2. X_ymin값이 같다면 기울기를 기준으로 판변
2_1. Del X를 기준으로 Del X가 작은것이 왼쪽에 위치
(y가 증가할 때 x가 감소하므로, 음의 기울기를 갖는 선분입니다)
이렇게 규칙을 통해서 완성된 다각형 테이블은 아래와 같습니다.
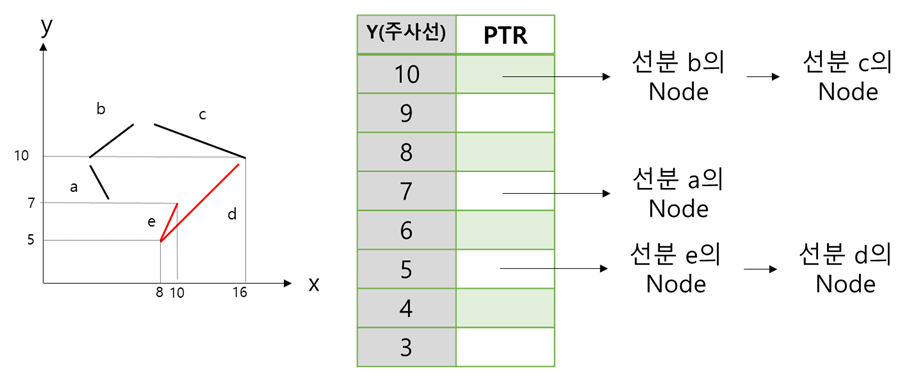
#Line을 입력받아서 해당 Line에 해당하는 Node를 형성합니다.
class node:
def __init__(self, Line, next_node):
self.x_ymin = Line[0][0] if Line[1][1]>Line[0][1] else Line[1][0]
x2 = Line[1][0] if Line[1][1]>Line[0][1] else Line[0][0]
self.y_max = Line[0][1] if Line[1][1]<Line[0][1] else Line[1][1]
y1 = Line[1][1] if Line[1][1]<Line[0][1] else Line[0][1]
self.del_x = (x2-self.x_ymin)/(self.y_max-y1)
self.next = next_node
del x2, y1
class fill_color:
#line의 input 형식은 [[x1,y1],[x2,y2],[x3,y3]...] 입니다.
def __init__(self, Line_list):
self.data =Line_list
#다각형 선분 테이블을 반들기 위해서
#선분들 중 가장 큰 Y값을 찾아줍니다.
max_y = 0
for i in range(len(self.data)):
if self.data[i][1]>max_y:
max_y = self.data[i][1]
self.link_list = [node([[999,998],[998,999]], None) for i in range(max_y)]
remove_index = []
for i in range(len(self.data)):
#만약 선분의 y값이 같으면 수평 선분이므로, 해당 선분을 제외해줍니다.
if self.data[i-1][1] == self.data[i][1]:
remove_index = remove_index + [i]
else:
#선분의 최상단 점은 제외 후 알고리즘을 적용하므로
#선분의 두 점중 낮은 값을 Index로 다각형 선분테이블에 추가합니다.
try_node = self.link_list[min(self.data[i-1][1],self.data[i][1])-1]
#이전 Node를 저장하기 위한 Dummy Node입니다.
before_node = node([[999,998],[998,999]], None)
while True:
if try_node.next == None:
try_node.next = node([self.data[i-1],self.data[i]], None)
before_node.next = try_node
break
elif try_node.next != None:
before_node = try_node
try_node = try_node.next
#구축된 선불리스트를 가지고 fill을 할 Pixel들을 계산합니다.
def cal(self):
current_list = []
for i in range(len(self.link_list)):
if self.link_list[i].next !=None:
this_node = self.link_list[i].next
while True:
current_list = current_list + [this_node]
if this_node.next == None:
break
else:
this_node = this_node.next
#현재 여기까지 구현, current_list를 가지고 채색을 하는 부분 구현 필요
return current_list
DT_list = [[50,70],[50,130],[80,220],[100,110],[150,70],[100,70],[80,90],[50,70]]
test = fill_color(DT_list)
temp = test.cal()
import matplotlib.pyplot as plt
plt.plot([50,50,80,100,150,100,80,50],[70,130,220,110,70,70,90,70])'컴퓨터과학 > 컴퓨터 그래픽스' 카테고리의 다른 글
| 8. 2차원 뷰잉 (0) | 2021.02.17 |
|---|---|
| 7. Color의 표현 (0) | 2021.02.16 |
| 5. 기하변환 3(복합기하변환, 아핀변환) (0) | 2021.02.13 |
| 4. 기하변환2(동차좌표ver) (0) | 2021.02.12 |
| 3. 기하변환1(기본기하변환) (0) | 2021.02.11 |
- Total
- Today
- Yesterday
- 동적계획법
- hash
- AVX
- stack
- ai
- Greedy알고리즘
- 코딩테스트
- javascript
- react
- 알고리즘
- git
- Python
- Sort알고리즘
- 이분탐색
- ChatGPT
- SIMD
- 자료구조
- 분할정복
- GPT
- 모바일청첩장
- 프로그래머스
- 사칙연산
- prime number
- 셀프모청
- 완전탐색 알고리즘
- GDC
- 청첩장
- Search알고리즘
- 병렬처리
- LLM
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
