티스토리 뷰
지난 포스팅에선 Point가 존재하는 화면을 Clipping 하는 방법에 대해서 확인하였습니다.
이번 포스팅은 2차원 평면에서 Line을 Clipping 하는 방법에 관련한 포스팅 입니다.
방법론 으론는
-. Cliping window를 기준으로 영역을 나눠서 판단하는 Cohen-Sutherland 선분 Clipping
-. 걱 선분마다 선분의 방정식을 매개변수로 표현하여 판단하는 Liang-Barsky 선분 Clipping
이 있습니다.
1. Cohen-Sutherland 선분 Clipping

해당 방법론은 Clipping Wnd를 중심에 두고, 좌우상하 와 대각선, 총 8개의 구역으로 나누게 됩니다.
이때 선분의 시작점과 끝점을 이어서 선분이 어떠한 영역에 위치하는지 확인하여 선분을 Clipping하게 됩니다.
이때 4가지 Case로 나눌 수가 있습니다.
1. 시작점과 끝점의 Node를 OR조합 했을 때 모두 0이 나오는 경우 => Clipping Wnd 내부에 존재
2. 시작점과 끝점의 Node를 AND조합 했을 때 0이 아님 => Clipping Wnd 외부에 존재
3. 시작 or 끝점이 Clipping Wnd 내부인데, 다른 한점이 외부에 있는 경우 => 추가 계산 필요
4. 시작, 끝점 모두 Clipping Wnd 외부에 존재하는데 AND 조합 시 0인 경우 => 추가 계산 필요
1번과 2번은 명확하게 유지 or 선분의 제거가 나뉩니다.
하지만 3번과 4번의 경우 교차하는 경계면이 하나 이상일 수 있기 때문에 여러번 Clipping을 진행해야합니다.

이제 1번 남기고, 2번 제끼고, 3번과 4번 Case의 선분에 대해서만 선분의 방정식을 만들고
xmin, xmax, ymin, ymax 수평, 수직 선분과의 교점을 구해주게 됩니다.
결국, 해당 방법론은 1,2번을 제외하고는 결국 선분의 방정식을 구한다는 점에서 많은 연산이 필요하게 됩니다.
2. Liang-Barsky 선분 Clipping
위에서 선분 3, 4번 Case는 결국 선분의 방정식을 구하고, 해당 방정식을 이용해서
Clipping Wnd와의 교점을 구해야 했습니다.
이번에는 모든 선분을 선분의 방정식으로 나타내고, 이 방정식을 특정 매개변수로 나타낼 것입니다.
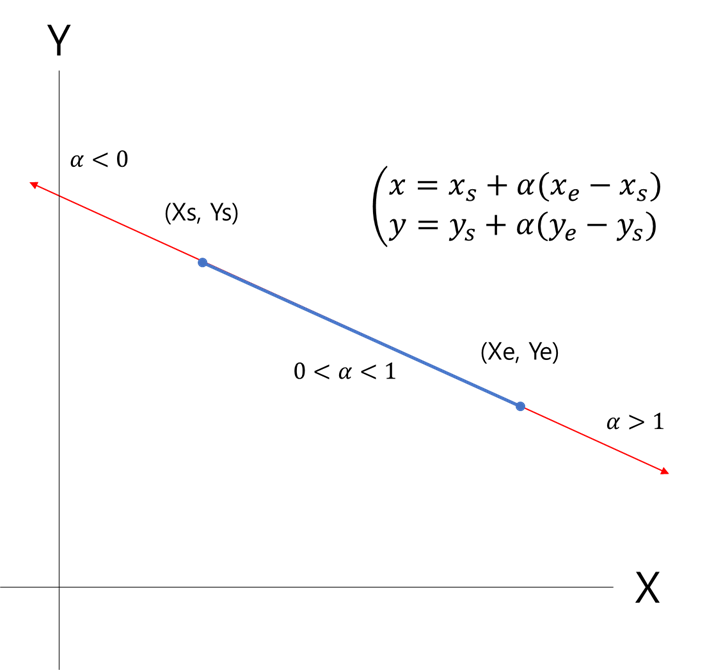
이렇게되면 Clipping Wnd의 xmax, xmin, ymax, ymin과의 교점을 위치를 모두 매개변수 알파로 나타낼 수가 있습니다.

위 경우는 Clipping Wnd 내에 두 점이 있을 경우입니다.
만약 알파가 0~1 사이가 아니라면, 다른 경계면과 만난다는것을 의미하게 됩니다.
그럼 이제 위의 선분의 방정식과 Clipping Wnd와의 교점에서의 알파를 구해주면
Clipping Wnd 대비 해당선분의 Position과 교점의 위치를 확인할 수 있겠죠?
그럼 이 교점으로 Xs, Xe, Ys, Ye를 갱신해주고 다시 Clipping을 진행하여 알파가 0~1 사이에 일을때까지 반복하면
최종적으로 Clipping 된 2차원 선분을 얻을 수가 있습니다 :)
python으로 구현된 Liang-Barsky 선분 Clipping입니다.
import copy
class line_clip:
#clipping Wnd는 [[Xmax,Xmin],[Ymax,Ymin]] 형식
def __init__(self, clipping_wnd):
self.x_max = clipping_wnd[0][0]
self.x_min = clipping_wnd[0][1]
self.y_max = clipping_wnd[1][0]
self.y_min = clipping_wnd[1][1]
#alpha 값을 받아서 해당 alpha값에 해당하는 x or y값을 반환합니다.
def line_eq(self, start, end, alpha, return_type):
if return_type == "y":
return start[1] + alpha*(end[1]-start[1])
elif return_type == "x":
return start[0] + alpha*(end[0]-start[0])
#상하, 좌우 Clipping 후 지속적으로 알파값을 갱신하기 위한 함수입니다.
def alpha_refresh(self, start, end):
#alpha를 가지고 Clipping을 진행하면서 지속적으로 start와 end의 값이 바뀌게 됩니다.
#이때 현재 alpha값은 갱신되기 전 start, end기준이기 때문에
#line_eq 함수에는 고정된 start, end값을 사용하기 위해서 임시로 저장해줍니다.
start_save = copy.deepcopy(start)
end_save = copy.deepcopy(end)
#float point 정확도 문제가 발생할 수가 있기 때문에 분자가 0인경우 0으로 고정값을 넣어줍니다.
left = 0 if (start[0]-self.x_min) == 0 else (start[0]-self.x_min)/(start[0]-end[0])
right = 0 if (self.x_max-start[0]) == 0 else (self.x_max-start[0])/(end[0]-start[0])
low = 0 if (start[1]-self.y_min) == 0 else (start[1]-self.y_min)/(start[1]-end[1])
high = 0 if (self.y_max-start[1]) == 0 else (self.y_max-start[1])/(end[1]-start[1])
return start_save, end_save, left, right, low, high
#Clipping이 진행된 후 현재 Clipping 된 선분의 알파값을 가지고 Clipping Wnd In/Out여부를 판단합니다.
def judge(self, start, end, left_a, right_a, low_a, high_a):
#start점이 end점 좌하단에 있는경우
if (start[0]<end[0] and start[1]<end[1])and((left_a<=0 and right_a>=1) and (low_a<=0 and high_a>=1)):
return start, end
#start점이 end점 좌상단에 있는경우
elif (start[0]<end[0] and start[1]>=end[1])and((left_a<=0 and right_a>=1) and (low_a>=1 and high_a<=0)):
return start, end
#start점이 end점 우하단에 있는경우
elif (start[0]>=end[0] and start[1]<end[1])and((left_a>=1 and right_a<=0) and (low_a<=0 and high_a>=1)):
return start, end
#start점이 end점 우상단에 있는경우
elif (start[0]>=end[0] and start[1]>=end[1])and((left_a>=1 and right_a<=0) and (low_a>=1 and high_a<=0)):
return start, end
#선분이 Clipping Wnd 외부에 존재하는 경우
if start[0] == None or start[1] == None or end[0] == None or end[1] == None:
return [None,None],[None,None]
#위 Case에 해당하지 않는경우 허수값을 반환하여 반복문(Clipping)을 계속 진행합니다.
return 999999
#[x,y]형태로 선분의 시작점과 끝점을 받습니다.
def cal(self, start, end):
while True:
#기본적인 start, end 지점에서 상하좌우 alpha값을 계산합니다.
start_temp, end_temp, left_a, right_a, low_a, high_a = self.alpha_refresh(start, end)
#start가 end보다 좌측에 있는 경우
if start[0]<=end[0]:
#Clipping Wnd의 x_min이 line 내에 있는 경우
#이경우 Clipping Wnd 의 x_min값이 Display할 최소 위치이므로
#start point의 X값을 clipping Wnd의 x값으로 최신화해줍니다.
if left_a>=0 and left_a<=1:
start[1] = self.line_eq(start_temp, end_temp, left_a, "y")
start[0] = self.x_min
#이 경우는 Line의 가장 왼쪽의 점이 이미 Clipping Wnd를 넘은 상황이므로
#None값을 부여해서 반복문을 종료하게 합니다.
elif left_a>1:
start[0] = None
if right_a>=0 and right_a<=1:
end[1] = self.line_eq(start_temp, end_temp, right_a, "y")
end[0] = self.x_max
#start가 end보다 우측에 있는 경우
elif start[0]>end[0]:
if left_a>=0 and left_a<=1:
end[1] = self.line_eq(start_temp, end_temp, left_a, "y")
end[0] = self.x_min
if right_a>=0 and right_a<=1:
start[1] = self.line_eq(start_temp, end_temp, right_a, "y")
start[0] = self.x_max
elif right_a<0:
start[0] = None
#좌우 Clipping을 한번 진행하고 알파를 최신화합니다.
start_temp, end_temp, left_a, right_a, low_a, high_a = self.alpha_refresh(start, end)
#결과를 기준으로 Line의 Status를 확인하여 Clipping 종료 여부를 판단
result = self.judge(start, end, left_a, right_a, low_a, high_a)
if result == 999999:
pass
else:
return start, end
#상하의 Clipping을 진행합니다.
if start[1]<=end[1]:
if low_a>=0 and low_a<=1:
start[0] = self.line_eq(start_temp, end_temp, low_a, "x")
start[1] = self.y_min
elif low_a>1:
start[1] = None
if high_a>=0 and high_a<=1:
end[0] = self.line_eq(start_temp, end_temp, high_a, "x")
end[1] = self.y_max
elif start[1]>end[1]:
if low_a>=0 and low_a<=1:
end[0] = self.line_eq(start_temp, end_temp, low_a, "x")
end[1] = self.y_min
if high_a>=0 and high_a<=1:
start[0] = self.line_eq(start_temp, end_temp, high_a, "x")
start[1] = self.y_max
elif right_a<0:
start[1] = None
#상하 Clipping을 한번 진행하고 알파를 최신화합니다.
start_temp, end_temp, left_a, right_a, low_a, high_a = self.alpha_refresh(start, end)
#결과를 기준으로 Line의 Status를 확인하여 Clipping 종료 여부를 판단
result = self.judge(start, end, left_a, right_a, low_a, high_a)
if result == 999999:
pass
else:
return start, end
#Clipping Wnd 영역 설정
wnd = [[20,10],[30,15]]
test = line_clip(wnd)
#Clipping을 할 Line을 설정합니다.
point = [[10,35],[14,5]]
#시각화를 위해서 start, end point 임시 저장
point_vis = copy.deepcopy(point)
result = test.cal(point[0],point[1])
import matplotlib.pyplot as plt
#Clipping Wnd를 Plot하고, 그 위에 Original Line과 Clipping 된 Line을 Plot합니다.
plt.plot([wnd[0][0],wnd[0][0]],[wnd[1][0],wnd[1][1]])
plt.plot([wnd[0][1],wnd[0][1]],[wnd[1][0],wnd[1][1]])
plt.plot([wnd[0][0],wnd[0][1]],[wnd[1][0],wnd[1][0]])
plt.plot([wnd[0][0],wnd[0][1]],[wnd[1][1],wnd[1][1]])
plt.plot([point_vis[0][0],point_vis[1][0]],[point_vis[0][1],point_vis[1][1]])
plt.plot([result[0][0], result[1][0]],[result[0][1], result[1][1]])
'컴퓨터과학 > 컴퓨터 그래픽스' 카테고리의 다른 글
| 8. 2차원 뷰잉 (0) | 2021.02.17 |
|---|---|
| 7. Color의 표현 (0) | 2021.02.16 |
| 6. 채색 알고리즘(수정중) (0) | 2021.02.15 |
| 5. 기하변환 3(복합기하변환, 아핀변환) (0) | 2021.02.13 |
| 4. 기하변환2(동차좌표ver) (0) | 2021.02.12 |
- Total
- Today
- Yesterday
- 청첩장
- 분할정복
- 알고리즘
- 프로그래머스
- git
- GPT
- Sort알고리즘
- hash
- javascript
- Greedy알고리즘
- 자료구조
- 병렬처리
- GDC
- 동적계획법
- LLM
- SIMD
- stack
- ai
- 이분탐색
- Search알고리즘
- prime number
- ChatGPT
- Python
- AVX
- 코딩테스트
- 셀프모청
- 모바일청첩장
- 완전탐색 알고리즘
- 사칙연산
- react
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
