티스토리 뷰

오늘 포스팅은 Python의 대표 Math Package중 하나인 Numpy에 대해서 다룹니다.
Python을 써보시면 아시겠지만, Python List 대비 Numpy Array의 연산이 훨신 빠르다는것을 알 수 있습니다.
Numpy가 왜 Native List보다 빠를 수 있는지, 하드웨어 관점을 더해서 설명합니다.
먼저 Numpy가 빠른 이유를 두줄 정리하고 갑니다.
- SIMD
- 데이터 정렬
1. SIMD
SIMD(Single Instruction Multi Data) 하나의 CPU 명령어로 두개 이상의 Data를 처리하는 방법을 의미합니다.

하지만 빠른 계산은 조상님이 해주는게 아닙니다.
CPU의 동작을 한번 생각해보겠습니다.

레지스터에는 하나에 하나의 32비트 2진수를 담을 수가 있습니다(General Purpose Register라고 합니다)
즉, SIMD 동작을 위해서는 한번 연산을 위해 필요한 범용레지스터의 개수가 증가하게 됩니다.
SIMD 동작을 위해서는 위 이미지에서 일부가 수정되어야 합니다.
-1. 범용레지스터의 개수가 많아지거나, 큰 데이터를 담을 특수 레지스터가 필요하다.
-2. ALU에서 다수 Data가 담긴 레지스터를 한번에 계산한 수 있어야 한다.
-3. 계산된 결과를 담을 누산기 역시 커져야 한다.
때문에, SIMD를 실행시키기 위해서 CPU에서 하드웨어적인 지원이 필수적으로 요구됩니다.
Intel 10세대 CPU의 DIE 중 SIMD Engine의 크기

SIMD는 현 세대 CPU에서 MMX(64), SSE(128), AVX(256), AVX512(512) 등 Instruction Set으로 불립니다
(이때 괄호안의 숫자는 범용레지스터의 총 Bit 수가 됩니다)
현재 인텔은 AVX512, AMD의 경우 AVX2까지 지원합니다.
(과거 셀러론이나 펜티엄 같은 저가 CPU에서는 위같은 SIMD 명령어들이 제거 되었습니다.
하지만 최신 CPU같은 경우 캐시크기와 pcie 대역폭 등의 차이가 나고, SIMD의 경우 큰 차이가 없어졌습니다.)
SIMD의 경우 변수 하나에 32bit 고정이 아니라, Int, Double, Float에 따라 가변적으로 레지스터를 쪼개서 사용합니다.
하지만, 아직 끝나지 않았습니다.
SIMD를 사용하기 위해서는 C/C++ 언어의 SIMD Intrinsic을 사용하여 코드를 구현해야 합니다.
아래는 C언어에서 Intel SIMD Intrinsic을 사용해서 AVX2를 사용, Array Add를 반복하는 코드입니다.
#include
#include // Intel core SIMD intrinsic instructions.
int main()
{
const int n = 10;
__m256i a, b, r, r_old;
__declspec(align(16)) long v1[8] = { 0, 22, 103, 14, 7, 12, 97, 10 };
__declspec(align(16)) long v2[8] = { 5, 11, 567, 35, 12, 18, 62, 12 };
__declspec(align(16)) long result[8] = { 0 };
for (int i = 0; i < n; ++i) {
a = _mm256_loadu_epi16(v1);
b = _mm256_loadu_epi16(v2);
r_old = _mm256_loadu_epi16(result);
r = _mm256_add_epi16(_mm256_add_epi16(a, b), r_old);
_mm256_storeu_epi16((__m256i*)result, r);
}
for (int c = 0; c < 8; c++) {
printf("%d ", result[c]);
}
}Numpy의 경우, Cpyhton으로 구현된 C 배열과, 이 배열의 SIMD 연산으로 비약적인 속도 상승을 얻을 수 있었습니다.
아래는 Numpy의 Ceil 연산을 위해서 C언어로 구현된 Ceil 연산 입니다.
SIMD Intrinsic을 활용해서 내부코드를 최적화 한 것을 알 수 있습니다(_mm으로 시작하는 함수들).
// ceil
#ifdef NPY_HAVE_SSE41
#define npyv_ceil_f32 _mm_ceil_ps
#define npyv_ceil_f64 _mm_ceil_pd
#else
NPY_FINLINE npyv_f32 npyv_ceil_f32(npyv_f32 a)
{
const npyv_f32 szero = _mm_set1_ps(-0.0f);
const npyv_f32 one = _mm_set1_ps(1.0f);
npyv_s32 roundi = _mm_cvttps_epi32(a);
npyv_f32 round = _mm_cvtepi32_ps(roundi);
npyv_f32 ceil = _mm_add_ps(round, _mm_and_ps(_mm_cmplt_ps(round, a), one));
// respect signed zero, e.g. -0.5 -> -0.0
npyv_f32 rzero = _mm_or_ps(ceil, _mm_and_ps(a, szero));
// if overflow return a
return npyv_select_f32(_mm_cmpeq_epi32(roundi, _mm_castps_si128(szero)), a, rzero);
}
NPY_FINLINE npyv_f64 npyv_ceil_f64(npyv_f64 a)
{
const npyv_f64 szero = _mm_set1_pd(-0.0);
const npyv_f64 one = _mm_set1_pd(1.0);
const npyv_f64 two_power_52 = _mm_set1_pd(0x10000000000000);
npyv_f64 sign_two52 = _mm_or_pd(two_power_52, _mm_and_pd(a, szero));
// round by add magic number 2^52
npyv_f64 round = _mm_sub_pd(_mm_add_pd(a, sign_two52), sign_two52);
npyv_f64 ceil = _mm_add_pd(round, _mm_and_pd(_mm_cmplt_pd(round, a), one));
// respect signed zero, e.g. -0.5 -> -0.0
return _mm_or_pd(ceil, _mm_and_pd(a, szero));
}
#endifsource code : numpy/core/src/common/simd/sse/math.h
2. 데이터 정렬
하지만, Numpy의 속도는 SIMD만으로는 설명이 되지 않습니다.
가장 최신SIMD인 AVX512는 512개의 2bit 레지스터가 있는 구조이기 때문에,
8비트 정수를 연산한다고 하면 512/8 = 64개,
32비트 정수를 연산한다고 하면 512/32 = 16개,
64비트 정수를 연산한다고 하면 512/64 = 8개의 Data를 동시에 처리할 수가 있습니다.
SIMD로 한번에 N배의 데이터를 처리하면, Python의 소요시간 = Numpy의 소요시간 * N이 나와야 합니다. 과연 그럴까요?
import numpy as np
import copy
import random
def np_add(a, b, ret):
ret = np.add(a, b)
return ret
def py_add(a, b):
ret = [i + j for i, j in zip(a, b)]
return ret
py_a = [float(random.randint(0, 1000)) for i in range(1000000)]
py_b = [float(random.randint(0, 1000)) for i in range(1000000)]
py_ret = [None for i in range(1000000)]
np_a = np.array(copy.deepcopy([np.float(i) for i in py_a]))
np_b = np.array(copy.deepcopy([np.float(i) for i in py_b]))
np_ret = np.array(copy.deepcopy(py_ret)).astype(np.float)
%timeit np_add(np_a, np_b, np_ret)
#==>3.34 ms ± 133 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
%timeit np_add(py_a, py_b, py_ret)
#==>136 ms ± 2.6 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
테스트 컴퓨터는 AVX2 까지만 지원합니다(256 bit 범용레지스터)
그렇다면, 64bit인 float을 한번에 4개씩 처리가 가능하고(64*4 = 256bit), 4배만큼만 빨라야합니다.
하지만 결과를 보면 136ms/3.4ms = 약 40배가 빠르다는것을 확인할 수 있습니다!
드디어 조상님이 계산을 대신 해주신걸까요?
아래 Numpy Array와 Python Array의 내부 구조를 잠시 비교해 보겠습니다.

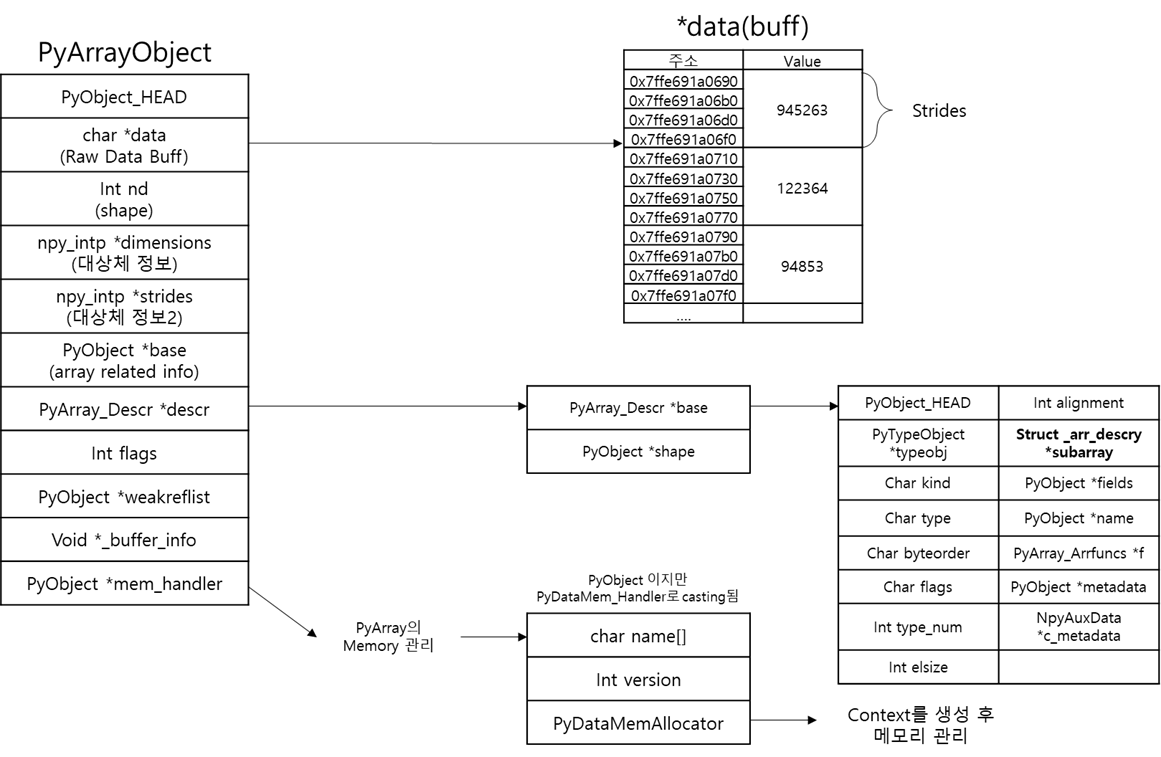
가장 대표적인 차이점으로, Python Array는 Item을 2중 포인터 형식으로 저장하며, 여기에 PyObject가 저장됩니다.
반면, Numpy의 경우 단일 포인터로 Buff의 첫 주소를 가리키고, Buff에서 ctype의 데이터가 C Array에 저장됩니다.
이 구조때문에 두가지 차이점이 발생합니다.
2_1. PyObject의 연산.
PyObject의 Binary 연산은 해당 사이트를 참고하시면 좋을것 같습니다(https://cyril.deguet.com/en/2015/06/15/how-python-code-is-executed/)
Python에서 Int, str, float으로 지정한 변수는 c언어 int, char, double과는 다릅니다.
최종적으로 포인터가 가리키는 값을 c언어의 그것과 비슷하지만, 해당 변수의 연산은 아래와 같이 inception이 들어갑니다.

이 과정에서 중간중간 type을 체크하는 다수의 예외처리가 존재하기 때문에, Ctype연산만으로 처리가 가능한 Numpy Array 대비 Python List의 연산은 느릴 수 밖에 없습니다
(c[i] = a[i] + b[i]을 한번 할때마다 위 과정이 필요하니깐요!)
2_2. 데이터의 지역성
잠시 지루한 이야기를 해 보겠습니다. 컴퓨터구조 수업을 들어보신 분들이라면, 아래와 같은 계층도를 잘 알고있을 겁니다.
출처 : https://computerscience.chemeketa.edu/cs160Reader/ComputerArchitecture/MemoryHeirarchy.html
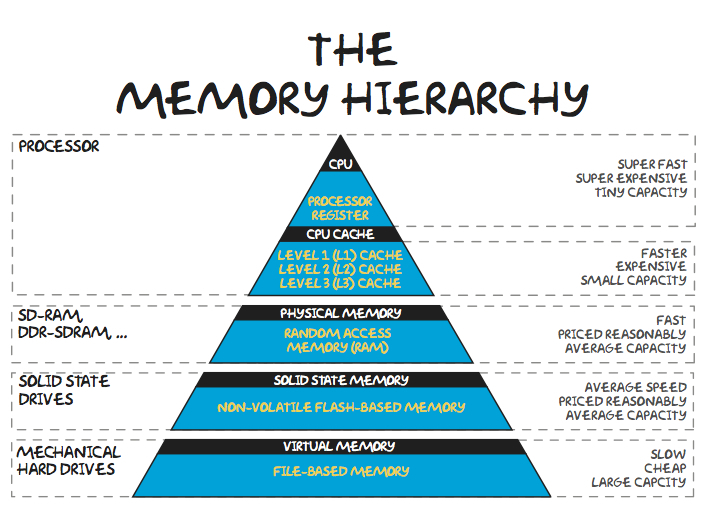
RAM이 아무리 빨라봐야 Cache보다 턱없이 느리고, Cache가 커봐야 램보다는 너무 작습니다.
이 문제를 해소하고자 CPU는 사용할 Data를 Cache에 저장해놓고, 빠르게 register로 가지고와서 계산을 진행합니다.
하지만, CPU가 Data를 찾을 때 Data가 Cache에 없으면 이 데이터를 RAM, 나아가서는 SSD에서 찾아야하고, 이는 엄청난 시간이 소요되게 됩니다.(이것을 Cache miss라고 합니다)
이러한 Cache miss를 방지하기 위해서 RAM과 Cache사이에는 Cache Line단위(일반적으로 64byte)로 필요한 데이터 + 주변의 데이터 통째로 가지고옵니다.
이때 Memory의 주변 Data를 사용할 확률이 높다는 점(Data의 공간지역성 이라고 합니다)을 활용해서 주변 데이터를 가지고 오게 됩니다

이런 지루한 이야기를 한 이유는, Python List와 Numpy Array의 연산속도의 차이를 만드는 나머지 부분이기 때문입니다.
Python List의 경우 PyListObject->PyObject->ob_item->.... 과 같은 형태로 되어있습니다. 때문에 여러번 memory allocation이 발생합니다.
즉, Python List a[0]과 a[1]의 PyObject를 가리키는 포인터주소는 메모리 상에서 인접하지만, 실제 데이터는 메모리 상에서 인접한다는 보장이 없습니다.

Python List의 위와같은 구조 때문에 Python List는 자체적으로 SIMD를 지원하지 않는 것으로 알려져있습니다.
(SIMD 연산을 위해서는 Data가 정렬되어 있어야 합니다)
반면, Numpy의 경우 미리 할당된 buff에 데이터가 C Array형태로 저장됩니다. 때문에 C malloc수준의 데이터 연속성을 보장받을 수 있습니다.
즉, Numpy Array는 Python List보다 cache hit rate가 높고, 이러한 다수의 요인이 겹쳐서 Numpy Array가 Python List보다 빠르다고 할 수 있겠습니다.
'Python 잡지식' 카테고리의 다른 글
| [Python]Uvicorn에 대해서 (0) | 2024.05.08 |
|---|---|
| [Python]Python 함수 실행간 메모리 측정하기 (0) | 2023.10.23 |
| Python의 함수 세부사항이 궁금할 때 (0) | 2021.03.21 |
| Python의 매개변수 전달방식 (0) | 2021.03.13 |
| Event Listener의 정체 (0) | 2021.03.10 |
- Total
- Today
- Yesterday
- 셀프모청
- ai
- 모바일청첩장
- hash
- prime number
- AVX
- 병렬처리
- 분할정복
- 알고리즘
- GDC
- 이분탐색
- 동적계획법
- 자료구조
- 프로그래머스
- Greedy알고리즘
- react
- Search알고리즘
- LLM
- 코딩테스트
- 사칙연산
- Python
- GPT
- git
- SIMD
- Sort알고리즘
- 청첩장
- stack
- 완전탐색 알고리즘
- ChatGPT
- javascript
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
