티스토리 뷰
컴퓨터의 화면은 점과 선 으로 이뤄져 있다고 할 수 있습니다.
(결국 선도 점으로 이뤄져 있죠)
이때, 컴퓨터는 어떻게 점과 선을 표현할까요?
이번 포스트는 컴퓨터가 점과 선을 표현하는 방법에 대한 포스트 입니다.
1. 점
2차원 평면에 점이 있다고 해 봅시다.
이때 기존에는 (x, y) 두개의 Element로 표현합니다.
이를 데카르트 좌표라고 합니다.
이때, 컴퓨터에선 점의 표현은 위해서 동차좌표라 하여, Element h를 추가한 좌표를 사용합니다.
데카르트 좌표 ==> 동차좌표
(x, y) ==> (xh, yh, h)
컴퓨터에서 점 표현에 동차좌표를 사용하는 이유는 추후 기하변환(회전, 수축, 이동 등)에서
h의 추가로 얻어지는 계산 및 편의성이 증가하기 때문입니다
(추후에 포스팅 예정입니다)
2. 선
선의 표현은 기존에 우리가 아주 잘 알고있습니다.
y = m * x + b (여기서 m은 기울기, b는 절편입니다)

그렇다면, 컴퓨터 내에서도 동일하게 두 점을 이용해서 기울기를 구하고, y와 x의 관계를 정의해 주면 됩니다.
2_1. DDA(Digital Differential Analyzer)
컴퓨터는 화면에 선을 표현해 주기 위해서 선을 점으로 쪼개서 표시해줘야 합니다.
DDA는 기울기의 값을 1 기준으로 나눠서 다르게 Point를 산출합니다.
1) 기울기가 1보다 큰 경우
이 경우 y값이 1 차이날 때 마다 x값을 산출해 줍니다.
(Yn+1 = Yn + 1, Xn+1 = Xn + 1/m, 이후 X값을 반올림)
2) 기울기가 1보다 작거나 같은경우
이 경우 x값이 1 차이날 때 마다 y값을 산출해 줍니다.
(Xn+1 = Xn +1, Yn+1 = Yn + m, 이후 Y값을 반올림)
방법은 간단하지만, DDA는 지속적으로 Float(실수)연산을 해야되기 때문에 연산시간이 증가합니다.
(=> 이미지가 화면에 표시되는데 시간이 오래걸리게 됩니다)
그리고 m을 더하면서 지속적으로 반올림을 진행하여, 실제 직선과의 오차가 발생하게 됩니다.
2_2 Bresenham의 직선 알고리즘(기울기가 0~1 사이라고 가정)

Bresenham의 직선 알고리즘은, x가 1 증가 할 때 그 다음의 점 중 기존 직선의 식과 가까운 것을 구하는 알고리즘 입니다.
이때 직접 해당 점의 위치의 선의 점을 구하는 것이 아니라, 판별식을 사용해서 Float연산을 피해갑니다.
시작점 x_s, y_s이 있고, 끝점 x_e, y_e가 있다고 생각해봅시다.
그럼 이 두 점의 직선의 방정식은

이때 실제 직선위에 y_real, x_real이 있다고 생각해봅니다.
y_real과 x_real의 값을 위 식에 대입하면
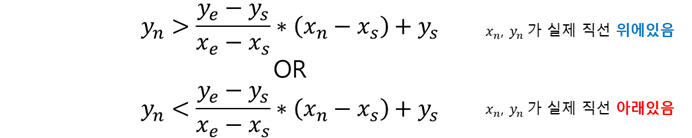
이제, 위 구해진 방법을 이용해서 x1, y1의 값마다 다음과같은 판별식을 만들 수 있습니다.

이제, x와 y에 주황점과 초록점의 중간값을 넣어주면(사진에선 x1+1과 y1+0.5)
그 결과가 판별식으로 나와서 0보다 큰지, 작은지를 알려주고
이를 통해서 float연산 없이 다음점의 위치를 구할 수 있습니다!
(판별식에 2를 곱해서 발생하는 1.5, 2.5....와 같은 X.5를 정수로 만들어줍니다)
판별식을 통해서 x,y 다음의 plot 위치를 구하고, 해당 위치에서 판변식을 진행하면
최종 Plot을 위한 픽셀의 위치를 산출할 수 있습니다.
python으로 구현한 DDA알고리즘과 Bresenham의 직선 알고리즘 입니다.
#기울기가 0이상인 경우만 구현하였습니다.
class DDA:
def __init__(self,DT_list):
self.ori_start = DT_list[0]
self.ori_end = DT_list[1]
self.slope = (self.ori_end[1]-self.ori_start[1])/(self.ori_end[0]-self.ori_start[0])
#다음 x,y값을 계산하기 위한 현재 x,y을 저장하는 속성을 선언합니다.
self.this_y = self.ori_start[0]
self.this_x = self.ori_start[1]
#정수화된 Plotting Point를 기록합니다.
self.route_point = []
def line_eq(self, x, y):
#line의 방정식을 정의하고
#이전의 x,y 값을 입력받아 slop에 따라 x or y값을 return합니다.
if self.slope <= 1 and self.slope > 0:
#기울기가 0~1 사이인 경우 기존의 y값에서 slope만급을 더해서 Int로 만들어 return
#이때 다음 계산을 위해서 Int가 아닌 float형태의 y도 같이 return합니다
return [round(self.slope + y,0),self.slope + y]
elif self.slope >1:
#기울기가 1보다 큰 경우 x값에다가 slope의 역수만큼을 더해서 Int로 만들어 return
#이때 다음 계산을 위해서 Int가 아닌 float형태의 x도 같이 return합니다
return [round(1/self.slope + x,0),1/self.slope + x,0]
def cal(self):
#x 또는 y가 end값에 도달하기 전까지 반복
while self.this_x < self.ori_end[0] and self.this_y < self.ori_end[1]:
#기울기가 0~1 인 경우
if self.slope <= 1 and self.slope > 0:
#line_eq를 사용해서, x+1에서의 y값을 반환받아 임시 저장합니다.
temp_next = [self.this_x+1,self.line_eq(self.this_x, self.this_y)]
#x+1과 x+1에서의 반올림된 y값을 plotting point로 저장합니다.
self.route_point = self.route_point + [[temp_next[0],temp_next[1][0]]]
#다음 point의 계산을 위해서 y와 x를 갱신합니다.(이때 갱신되는 y는 float형태)
self.this_x, self.this_y = [temp_next[0],temp_next[1][1]]
#기울기가 1이상 인 경우
elif self.slope >1:
#line_eq를 사용해서, y+1에서의 x값을 반환받아 임시 저장합니다.
temp_next = [self.line_eq(self.this_x, self.this_y),self.this_y+1]
#y+1과 y+1에서의 반올림된 x값을 plotting point로 저장합니다.
self.route_point = self.route_point + [[temp_next[0][0],temp_next[0]]]
#다음 point의 계산을 위해서 y와 x를 갱신합니다.(이때 갱신되는 x는 float형태)
self.this_x, self.this_y = [temp_next[0][1],temp_next[0]]
return self.route_point
#[x,y] 2차워 좌표계[start, end]
test_point = [[0,0],[128,72]]
test = DDA(test_point)
import matplotlib.pyplot as plt
#정수화된 Point를 가지고 Plot한 결과를 도시합니다.
plt.scatter([i[0] for i in test.cal()],[i[1] for i in test.cal()], s=10)
#실제 Line을 도시하여 비교합니다.
plt.axline(test_point[0],test_point[1], color = "r")
#기울기가 0~1 사이일 때만 구현하였습니다.
class bresen:
def __init__(self,DT_list):
self.ori_start = DT_list[0]
self.ori_end = DT_list[1]
self.h, self.w = [(self.ori_end[1]-self.ori_start[1]),(self.ori_end[0]-self.ori_start[0])]
#다음 x,y값을 계산하기 위한 현재 x,y을 저장하는 속성을 선언합니다.
self.this_y = self.ori_start[0]
self.this_x = self.ori_start[1]
#정수화된 Plotting Point를 기록합니다.
self.route_point = []
def j_eq(self, x, y):
if 2*self.h*(x+1-self.ori_start[1]) - 2*self.w*(y+0.5-self.ori_start[0])<=0:
return [self.this_x+1, self.this_y]
elif 2*self.h*(x+1-self.ori_start[1]) - 2*self.w*(y+0.5-self.ori_start[0])>0:
return [self.this_x+1, self.this_y+1]
def cal(self):
while self.this_x < self.ori_end[0] and self.this_y < self.ori_end[1]:
temp_next = self.j_eq(self.this_x, self.this_y)
self.route_point = self.route_point + [temp_next]
self.this_x, self.this_y = temp_next
return self.route_point
#[x,y] 2차워 좌표계[start, end]
test_point = [[0,0],[128,72]]
test = bresen(test_point)
test.cal()
import matplotlib.pyplot as plt
#정수화된 Point를 가지고 Plot한 결과를 도시합니다.
plt.scatter([i[0] for i in test.cal()],[i[1] for i in test.cal()], s=10)
#실제 Line을 도시하여 비교합니다.
plt.axline(test_point[0],test_point[1], color = "r")
'컴퓨터과학 > 컴퓨터 그래픽스' 카테고리의 다른 글
| 6. 채색 알고리즘(수정중) (0) | 2021.02.15 |
|---|---|
| 5. 기하변환 3(복합기하변환, 아핀변환) (0) | 2021.02.13 |
| 4. 기하변환2(동차좌표ver) (0) | 2021.02.12 |
| 3. 기하변환1(기본기하변환) (0) | 2021.02.11 |
| 2. 곡선과 원 (0) | 2021.02.10 |
- Total
- Today
- Yesterday
- GDC
- 모바일청첩장
- 이분탐색
- 셀프모청
- hash
- stack
- 자료구조
- javascript
- Python
- GPT
- AVX
- 분할정복
- Sort알고리즘
- 청첩장
- ai
- git
- 완전탐색 알고리즘
- react
- Greedy알고리즘
- 프로그래머스
- 병렬처리
- ChatGPT
- 알고리즘
- SIMD
- Search알고리즘
- 동적계획법
- prime number
- 사칙연산
- LLM
- 코딩테스트
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |

